非线性优化（一）：优化方法_米乐体育馆陶瓷研磨抛光站

非线性优化（一）：优化方法

发布时间：2024-08-26 来源：网络

讲完了李群和李代数，就轮到最小二乘优化了。和之前一样，应该会是一系列文章。这一章就先讲讲一些基本的概念和常见的最小二乘算法。

一个最小二乘问题的定义如下：

寻找一个关于下列函数的局部最小值 $\\mathbf{x}^*$ ：

$F(x)=\\frac{1}{2}\\sum^m_{i=1}(f_i (\\mathbf{x}) )^2 \\quad f_i: \\mathbf{R}^n \ o \\mathbf{R}, \\quad m \\ge n$

这里， $f_i ( \\mathbf{x})$ 是误差方程。

而局部最小值的定义为：

给定 $F: \\mathbf{R}^n \ o \\mathbf{R}$ ，找到一个 $\\mathbf{x}^*$ ，使得

$F(\\mathbf{x}^*) \\le F(\\mathbf{x}) \\quad \ ext{for}\\ || \\mathbf{x}- \\mathbf{x}^* || < \\delta$

这里， $\\delta$ 是一个给定的小正数。

假设损失函数F是光滑、可微的，就可以对其进行泰勒展开:

$F(\\mathbf{x}+ \\mathbf{h})=F(\\mathbf{x}) + \\mathbf{h}^T \\mathbf{g}+ \\frac{1}{2}\\mathbf{h}^T \\mathbf{H}\\mathbf{h}+ O(|| \\mathbf{h}||^3)$

其中，g是一阶导数（gradient）：

$g=F' (\\mathbf{x})=\\begin{bmatrix}\\frac{\\partial F}{\\partial x_1}(\\mathbf{x}) \\\\ \\\\ \\frac{\\partial F}{\\partial x_2}(\\mathbf{x}) \\\\ \\\\ \\vdots \\\\ \\frac{\\partial F}{\\partial x_n}(\\mathbf{x}) \\\\ \\end{bmatrix}$

而H为海塞矩阵（Hessian）

$\\mathbf{H}=F''(\\mathbf{x})=\\begin{bmatrix}\\frac{ \\partial^2 F }{\\partial x_i \\partial x_j }(\\mathbf{x}) \\end{bmatrix}$

显然，如果 $\\mathbf{x}^*$ 是一个局部最小值且 $||\\mathbf{h}||$ 足够小，那么我们不可能再找到一个更小的 $F(\\mathbf{x}^* + \\mathbf{h})$ 。

如此，可以先给出一个局部极小值的必要条件：

如果 $\\mathbf{x}^*$ 是一个局部极小值，那么 $\\mathbf{g}^*=F'(\\mathbf{x}^*)=0$ 。

我们知道，满足上述条件的点包括：局部极小值，局部极大值和鞍点，统称为驻点（stationary point）。为了判断一个驻点 $\\mathbf{x}_s$ 是否是一个局部极小值，将之反代回F的泰勒展开式：

$F( \\mathbf{x}_s + \\mathbf{h})=F( \\mathbf{x}_s ) + \\frac{1}{2}\\mathbf{h}^T \\mathbf{H}_s \\mathbf{h}+ h.o.t$

由海塞矩阵的定义可知，H是一个对称矩阵。如果它同时是一个正定矩阵的话，那么其特征值会大于某个数值 $\\delta > 0$ ，并且

$\\frac{1}{2}\\mathbf{h}^T \\mathbf{H}_s \\mathbf{h}> \\delta ||\\mathbf{h}|| ^2$

显然，此时 $F(\\mathbf{x}_s + \\mathbf{h}) > F(\\mathbf{x}_s)$ 。

由此，可以得到一个局部最小值的充分条件:

假定 $\\mathbf{x}^*$ 是一个驻点，且 $F''(\\mathbf{x}^*)$ 是一个正定矩阵，那么 $\\mathbf{x}^*$ 是一个局部极小值。

显然，如果H是一个负定矩阵，那么x是一个局部极大值；如果H既有正的特征值，又有负的特征值，那么s就是个鞍点。

对于非线性优化方法，其解法基本都是迭代方法：给定一个起始点 $\\mathbf{x}_0$ ，不断迭代产生新的 $\\mathbf{x}_1, \\mathbf{x}_2 \\dots$ ，并最终收敛至 $\\mathbf{x}^*$ 。为此，引入下降条件（decending condition）：

$F(\\mathbf{x}_{k+1}) < F(\\mathbf{x}_k)$

回到F的泰勒展开式，我们有

$F(\\mathbf{x}+ \\alpha \\mathbf{h}) \\approx F(\\mathbf{x}) + \\alpha \\mathbf{h}^T \\mathbf{F}' (\\mathbf{x})$

可以看到，如果 $\\mathbf{h}^T \\mathbf{F}' (\\mathbf{x}) < 0$ ，那么h就是F的一个下降方向。

很显然，基本所有下降方法都可以概括为以下两步：

1. 找到一个下降方向 $\\mathbf{h}_d$ ，然后

2. 找到一个迭代步长使得F的值减小；

其中，这个步长 $\\alpha$ 可以通过线性搜索（line search）的方式得到。

由前面的等式可以得到

$\\lim_{\\alpha \ o 0}\\frac{F(\\mathbf{x}) - F(\\mathbf{x}+ \\alpha \\mathbf{h}) }{\\alpha ||\\mathbf{h}||}=\\frac{1}{||\\mathbf{h}||}\\mathbf{h}^T \\mathbf{F}'(\\mathbf{x})=-||\\mathbf{F}'(\\mathbf{x})|| \\cos \ heta$

该方程表示的是方程F的相对下降（relative gain）。可以发现，它在 $\ heta=\\pi$ 的时候可以获得最大的下降。

由此，可以得到最速下降法的下降方向

$\\mathbf{h}_{sd}=-\\mathbf{F}'(\\mathbf{x})$

最速下降法的特点是在刚开始的阶段有较好的表现，但是到了最后是线性收敛。

对此，也诞生了混合方法（hybrid methods）：在开始阶段使用一种方法，在最后阶段使用另一种方法。

我们知道，对于局部极小值有 $\\mathbf{F}'(\\mathbf{x}^*)=0$ 。这是一个非线性方程组，为此，对其进行泰勒展开有：

$\\mathbf{F}'(\\mathbf{x}+ \\mathbf{h}) \\approx \\mathbf{F}'(\\mathbf{x}) + \\mathbf{F}''(\\mathbf{x}) \\mathbf{h}$

令上式等于0就可以得到牛顿法：

$\\mathbf{H}\\mathbf{h}_n=-\\mathbf{F}'(\\mathbf{x})$

下次迭代就有

$\\mathbf{x}:=\\mathbf{x}+ \\mathbf{h}_n$

如果H是正定的（说明上式具有唯一解），即对于所有 $\\mathbf{u}>0$ 有 $\\mathbf{u}^T \\mathbf{H}\\mathbf{u}>0$ ，则有

$0 < \\mathbf{h}^T_n \\mathbf{H}\\mathbf{h}_n=-\\mathbf{h}^T_n \\mathbf{F}'(\\mathbf{x})$

说明 $\\mathbf{h}_n$ 是损失函数F的一个下降方向。

牛顿法在最后的收敛阶段有很好的表现，在一定条件下（局部最小值附近的H是正定的且x已接近局部最小值），其可以达到二次收敛。

问题在于，如果H是负定的，且附近有一个局部最大值，牛顿法可能会收敛至该局部最大值。我们可以要求损失函数每一步都是减小的，或者使用如下的混合方法：

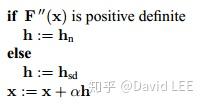
使用一个模型L来拟合F在其临域内的行为，则有

$F(\\mathbf{x}+ \\mathbf{h}) \\approx L(\\mathbf{h})=F(\\mathbf{x}) + \\mathbf{h}^T \\mathbf{c}+ \\frac{1}{2}\\mathbf{h}^T \\mathbf{B}\\mathbf{h}$

可以看到，L是F的二次泰勒展开式的一个近似。其中，c来近似梯度，而B为近似的海塞矩阵。

对于置信区域法，我们认为这个模型L在一个限定范围 $\\Delta$ 内是足够精确的。如此，就可以得到对应的下降方向

$\\mathbf{h}=\\mathbf{h}_{tr}=\\arg\\min_{||h|| < \\Delta}\\{ L(\\mathbf{h}) \\}$

而对于阻尼法，有

$\\mathbf{h}=\\mathbf{h}_{dm}=\\arg\\min_h \\{ L(\\mathbf{h}) + \\frac{1}{2}\\mu \\mathbf{h}^T \\mathbf{h}\\}$

阻尼因子 $\\mu \\ge 0$ ，该阻尼是用来惩罚大步长的。

算法2.4就可以变为

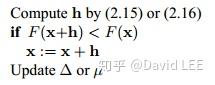
其实就是如果h满足下降条件，则 $\\alpha=1$ ；否则 $\\alpha=0$ 。并且通过调整 $\\Delta$ 或 $\\mu$ ，算法可以避免被困在某一点。

考虑到L是对F的临域的模拟，算法更新失败可能就是h（步长）太大了，导致近似不太好。为了衡量L对F的拟合度，定义一个gain ratio

$\\rho=\\frac{F(\\mathbf{x}) - F(\\mathbf{x}+ \\mathbf{h})}{L(0) - L(\\mathbf{h})}$

$\\rho$ 表示的是损失函数真实下降值和预计下降值之间的比例。由于分母是正数，当分子很小或者为负时，说明此时损失函数没有下降多少甚至还上升来，我们就知道当前的h太大了，导致L不是一个好的近似。

对于置信区域法和阻尼法，常见的更新策略为

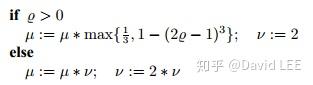
算法对于其中的常数的设置并不敏感，重要的是选择合适的值使得 $\\Delta$ 或 $\\mu$ 不震荡。

前面的损失函数还可以展开为如下形式：

$F(\\mathbf{x})=\\frac{1}{2}\\sum_{i=1}^m (f_i (\\mathbf{x}) )^2=\\frac{1}{2}|| \\mathbf{f}( \\mathbf{x}) ||^2=\\frac{1}{2}\\mathbf{f}( \\mathbf{x})^T \\mathbf{f}( \\mathbf{x})$

误差函数f(x)的泰勒展开式为：

$\\mathbf{f}( \\mathbf{x}+ \\mathbf{h})=\\mathbf{f}( \\mathbf{x}) + \\mathbf{J}( \\mathbf{x}) \\mathbf{h}+ O ( || \\mathbf{h}||^2 )$

其中，雅可以矩阵J可以写为

$( \\mathbf{J}( \\mathbf{x}) )_{ij}=\\frac{ \\partial f_i }{ \\partial x_j }( \\mathbf{x})$

如此一来，损失函数F的微分就可以写成：

$\\frac{ \\partial F }{ \\partial x_j }( \\mathbf{x})=\\sum_{i=1}^m f_i ( \\mathbf{x}) \\frac{ \\partial f_i }{ \\partial x_j }( \\mathbf{x})$

将它写成矩阵的形式就有：

$\\mathbf{F}' ( \\mathbf{x})=\\mathbf{J}( \\mathbf{x})^T \\mathbf{f}( \\mathbf{x})$

最后，F的二阶导（海塞矩阵）为：

$\\begin{aligned}\\mathbf{F}'' ( \\mathbf{x}) &=\\frac{ \\partial ^2 F }{ \\partial x_j \\partial x_k }( \\mathbf{x})=\\sum_{i=1}^m ( \\frac{ \\partial f_i }{ \\partial x_j }( \\mathbf{x}) \\frac{ \\partial f_i }{ \\partial x_k }( \\mathbf{x}) + f_i ( \\mathbf{x}) \\frac{ \\partial ^2 f_i }{ \\partial x_j \\partial x_k }( \\mathbf{x}) ) \\\\ &=\\mathbf{J}( \\mathbf{x})^T \\mathbf{J}( \\mathbf{x}) + \\sum_{i=1}^m f_i ( x ) \\mathbf{f}''_i ( \\mathbf{x}) \\end{aligned}$

GN算法基于对误差函数f的线性近似：

$\\mathbf{f}( \\mathbf{x}+ \\mathbf{h}) \\approx \\mathbf{l}( \\mathbf{h})=\\mathbf{f}( \\mathbf{x}) + \\mathbf{J}( \\mathbf{x}) \\mathbf{h}$

因此，损失函数F就变为

$\\begin{aligned}F( \\mathbf{x}+ \\mathbf{h}) \\approx L ( \\mathbf{h}) &=\\frac{1}{2}\\mathbf{l}( \\mathbf{h})^T \\mathbf{l}( \\mathbf{h}) \\\\ &=\\frac{1}{2}\\mathbf{f}^T \\mathbf{f}+ \\mathbf{h}^T \\mathbf{J}^T \\mathbf{f}+ \\frac{1}{2}\\mathbf{h}^T \\mathbf{J}^T \\mathbf{J}\\mathbf{h}\\\\ &=F( \\mathbf{x}) + \\mathbf{h}^T \\mathbf{J}^T \\mathbf{f}+ \\frac{1}{2}\\mathbf{h}^T \\mathbf{J}^T \\mathbf{J}\\mathbf{h}\\end{aligned}$

L 的梯度和海塞矩阵就是：

$\\mathbf{L}' ( \\mathbf{h})=\\mathbf{J}^T \\mathbf{f}+ \\mathbf{J}^T \\mathbf{J}\\mathbf{h}\\quad \\mathbf{L}'' ( \\mathbf{h})=\\mathbf{J}^T \\mathbf{J}$

而且，如果梯度J是满秩的，那么L的海塞矩阵H就是正定的，说明L(h)拥有唯一的极小值。

通过令L'(h)=0就可以得到GN算法的解：

$(\\mathbf{J}^T \\mathbf{J}) \\mathbf{h}_{gn}=- \\mathbf{J}^T \\mathbf{f}$

可以证明， $\\mathbf{h}_{gn}$ 确为损失函数F的下降方向：

$\\mathbf{h}_{gn}^T \\mathbf{F}' ( \\mathbf{x})=\\mathbf{h}_{gn}^T ( \\mathbf{J}^T \\mathbf{f})=-\\mathbf{h}_{gn}^T ( \\mathbf{J}^T \\mathbf{J}) \\mathbf{h}_{gn}< 0$

上一小节提到过，牛顿法可以达到二次收敛。但GN法却不行。为此，我们可以对比这两种方法：

$\\mathbf{F}''(x) \\mathbf{h}_n=-\\mathbf{F}'(x) \\quad \ ext{and}\\quad \\mathbf{L}'' (\\mathbf{h}) \\mathbf{h}_{gn}=-\\mathbf{L}'(0)$

已知这两个等式的右边是一样的，但是等式左边却是不一样的：

$\\mathbf{F}'' ( \\mathbf{x})=\\mathbf{L}'' ( \\mathbf{h}) + \\sum_{i=1}^m f_i ( x ) \\mathbf{f}''_i ( \\mathbf{x})$

显然，如果 $\\mathbf{f}( \\mathbf{x}^* )=0$ ，那么当x接近x*时， $\\mathbf{L}'' (\\mathbf{h}) \\backsimeq \\mathbf{F}''(x)$ 。此时，GN算法可以有二次收敛；但更多时候，GN算法只能达到线性收敛。

LM算法是阻尼法的一种，其步长可以这么算出：

$( \\mathbf{J}^T \\mathbf{J}+ \\mu \\mathbf{I}) \\mathbf{h}_{lm}=-\\mathbf{g}\\quad \ ext{with}\\ \\mathbf{g}=- \\mathbf{J}^T \\mathbf{f}\\ \ ext{and}\\ \\mu \\ge 0$

其中，u是拉格朗日算子，它有以下作用：

1. 对于u > 0，可以保证系数矩阵是正定的。这就保证了 $\\mathbf{h}_{lm}$ 必然是一个下降方向；

2. 如果u值很大，那么 $\\mathbf{h}_{lm}\\backsimeq - \\frac{1}{\\mu}\\mathbf{g}=-\\frac{1}{\\mu}\\mathbf{F}' ( \\mathbf{x})$ . 这是最速下降法下的一小步。这应用在当前迭代距离结果很远的时候；

3. 如果u值很小，那么 $\\mathbf{h}_{lm}\\simeq \\mathbf{h}_{gn}$ ，说明当前的线性近似比较准确。

因此，阻尼因子同时影响了当前迭代的方向和步长。其更新方式在前面已经介绍过了，而初始值可以根据 $\\mathbf{A}_0=\\mathbf{J}^T(\\mathbf{x}_0) \\mathbf{J}(\\mathbf{x}_0)$ 中元素的大小给出：

$\\mu_0=\ au \\cdot \\max_i \\{ a^{(0)}_{ii}\\}$

对于 $\ au$ 的选择，如果起始点x0是对结果的一个比较好的近似， $\ au$ 应该选取一个比较小的值，如 $10^{-6}$ ；否则，可以选择 $\ au=10^{-3}$ 或者 $\ au=1$ .

其更新策略同样是计算gain ratio：

$\\rho=\\frac{F(\\mathbf{x}) - F(\\mathbf{x}+ \\mathbf{h}_{lm})}{L(0) - L(\\mathbf{h}_{lm})}$

其中，

$\\begin{aligned}L(0) - L(\\mathbf{h}_{lm})&=-\\mathbf{h}_{lm}^T \\mathbf{J}^T \\mathbf{f}- \\frac{1}{2}\\mathbf{h}_{lm}^T \\mathbf{J}^T \\mathbf{J}\\mathbf{h}_{lm}\\\\ &=-\\frac{1}{2}\\mathbf{h}_{lm}^T ( 2 \\mathbf{g}+ (\\mathbf{J}^T \\mathbf{J}+ \\mu \\mathbf{I}- \\mu \\mathbf{I}) \\mathbf{h}_{lm}) \\\\ &=\\frac{1}{2}\\mathbf{h}_{lm}^T ( \\mu \\mathbf{h}_{lm}- \\mathbf{g}) \\end{aligned}$

注意到等式最后两项必然是正的，因此，就像前面说的， $\\rho$ 的值取决于F的增量。

最后，LM算法的流程如下：

首先，当算法到达一个最小值时，有 $\\mathbf{F}' ( \\mathbf{x}^* )=\\mathbf{g}( \\mathbf{x}^* )=0$ 。因此，第一种停止条件可以为

$|| \\mathbf{g}||_\\infty \\le \\epsilon_1$

这里， $\\epsilon_1$ 是一个很小的正数。

此外，第二种停止条件为在x变化很小时停止：

$|| \\mathbf{x}_{new}- \\mathbf{x}|| \\le \\epsilon_2 ( || \\mathbf{x}|| + \\epsilon_2 )$

这说明了在x数值较大时，使用前者（相对量）来说为停止条件；在x数值较小时，使用后者（绝对量）来作为停止条件。

最后，还可以限制迭代次数：

$k \\ge k_{max}$

我们已经知道，GN算法通过求解如下等式（normal equation）得到迭代方向和步长：

$\\mathbf{J}^T \\mathbf{J}\\mathbf{h}_{gn}=- \\mathbf{J}^T \\mathbf{f}$

而最速下降法则用逆梯度方向作为迭代方向：

$\\mathbf{h}_{sd}=- \\mathbf{g}=- \\mathbf{J}^T \\mathbf{f}$

其步长可以通过以下方式得到：

$\\mathbf{f}( \\mathbf{x}+ \\alpha \\mathbf{h}_{sd}) \\simeq \\mathbf{f}( \\mathbf{x}) + \\alpha \\mathbf{J}\\mathbf{h}_{sd}$

对损失函数则有

$F( \\mathbf{x}+ \\alpha \\mathbf{h}_{sd}) \\simeq \\frac{1}{2}|| \\mathbf{f}( \\mathbf{x}) + \\alpha \\mathbf{J}\\mathbf{h}_{sd}|| ^2=F( \\mathbf{x}) + \\alpha \\mathbf{h}_{sd}^T \\mathbf{J}^T \\mathbf{J}\\mathbf{f}+ \\frac{1}{2}\\alpha^2 || \\mathbf{J}\\mathbf{h}_{sd}||^2$

通过对上式进行求导，并令导数为0可得

$\\alpha=-\\frac{ \\mathbf{h}_{sd}^T \\mathbf{J}^T \\mathbf{f}}{ || \\mathbf{J}\\mathbf{h}_{sd}|| ^2 }=\\frac{|| \\mathbf{g}||^2 }{ || \\mathbf{J}\\mathbf{g}||^2 }$

这样一来，在更新x的时候，我们就有两个可选的解了： $\\mathbf{a}=\\alpha \\mathbf{h}_{sd}$ 和 $\\mathbf{b}=\\mathbf{h}_{gn}$ 。

而狗腿法是一种置信区域方法。其选取迭代方向和步长的方法如下图所示：

通过上图可以发现，还有一个参数 $\\beta$ 没有确定。令 $c=\\mathbf{a}^T ( \\mathbf{b}- \\mathbf{a})$ ，和

$\\psi(\\beta)=|| \\mathbf{a}+ \\beta ( \\mathbf{b}- \\mathbf{a}) ||^2 - \\Delta^2=|| \\mathbf{b}- \\mathbf{a}||^2 \\beta^2 + 2 c \\beta + || \\mathbf{a}|| - \\Delta^2$

则有

$\\begin{cases}\\beta=(-c + \\sqrt{c^2 + ||\\mathbf{b}- \\mathbf{a}||^2 (\\Delta^2 - ||\\mathbf{a}||^2)}) / || \\mathbf{b}- \\mathbf{a}||^2 & \\quad c \\le 0 \\\\ \\beta=(\\Delta^2 - ||\\mathbf{a}||^2) / (c + \\sqrt{c^2 + ||\\mathbf{b}- \\mathbf{a}||^2 (\\Delta^2 - ||\\mathbf{a}||^2)}) & \\quad c > 0 \\end{cases}$

最终的算法如下图所示

参考文献：METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS

如果觉得有用，还请点个赞: )

新闻中心

非线性优化（一）：优化方法